Codility Lesson 11 - CountNonDivisible(JAVA)

https://app.codility.com/programmers/lessons/11-sieve_of_eratosthenes/count_non_divisible/

CountNonDivisible coding task - Learn to Code - Codility

 

문제

- 배열 A가 주어지며, N개의 정수들로 이루어져 있다.

- 배열 A의 각 원소들에서 나누어지지 않는 수들의 개수를 구하라.

- 예시 : A[0] = 3 A[1] = 1 A[2] = 2 A[3] = 3 A[4] = 6

• A[0] = 3, the non-divisors are: 2, 6,
• A[1] = 1, the non-divisors are: 3, 2, 3, 6,
• A[2] = 2, the non-divisors are: 3, 3, 6,
• A[3] = 3, the non-divisors are: 2, 6,
• A[4] = 6, there aren't any non-divisors.

return [2, 4, 3, 2, 0]

 

제한조건

• N is an integer within the range [1..50,000];
• each element of array A is an integer within the range [1..2 * N].

N은 1 ~ 50,000 사이의 정수이다.( 빈 배열이 없다 )

A배열의 각 원소들은 1 ~ 2*N 사이의 정수이다.

 

풀이

- N이 1개일 경우에는 나눌 수가 없으므로 return [0]

- int[] table 배열을 만든다( table에는 count한 수를 저장 )

- copyA( A배열을 복사 )를 sort 시킨 후 for문으로 뒤쪽부터 순회한다.

- 자신보다 큰 수는 나눌 수 없는 수임으로 배제하고 그 아래 수들만 비교하여 나눌수 없는 수를 카운트한다.

- 그 아래 수들을 비교할 때, 같은 수를 만나면 break

- table에 수가 있는지 확인하고, 수가 없을 경우 갱신한다.

 

결과

 

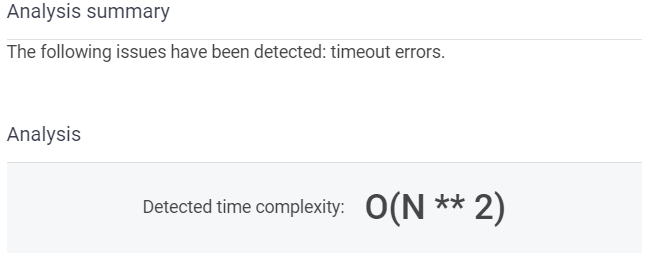
time out 에러...

 

소스코드( 1트 )

// you can also use imports, for example:
import java.util.*;

// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");

class Solution {
    public int[] solution(int[] A) {
        // write your code in Java SE 8
        int N = A.length;

        int[] answer = new int[N];
        // 0. 예외처리
        if( N < 2 ){
            answer[0] = 0;
            return answer;
        }

        // 1. A배열을 복사
        int[] copyA = Arrays.copyOfRange(A, 0, A.length);

        Arrays.sort(copyA);
        int[] table = new int[2*N + 1];

        int overNum = 0;
        int sameNum = 0;
        int prev = 2 * N + 1;
        for( int i=N-1; i>=0; i-- ){
            if( prev == copyA[i] ){
                sameNum += 1;
            }else{
                sameNum = 0;
            }

            int nonNum = 0;
            // 아래에 있는 수만 파악
            for( int j=0; j<i; j++ ){
                // System.out.println("copyA[i] : " + copyA[i] + " / copyA[j] : " + copyA[j]);
                if( copyA[i] == copyA[j] ) break;

                if( copyA[i] % copyA[j] != 0 ){
                    nonNum += 1;
                }
            }

            // System.out.println("nonNum : " + nonNum + " / overNum : " + overNum + " / sameNum : " + sameNum);
            table[copyA[i]] = nonNum + overNum - sameNum;

            overNum += 1;
            prev = copyA[i];
        }

        for( int i=0; i<N; i++ ){
            answer[i] = table[A[i]];
        }

        return answer;
    }
}

 

소스코드( 2트 )

- table에 저장된 수는 고려하지 않는 걸 추가함( 결국 같은 수는 같은 nondivisible을 갖게 됨으로 )

 

// you can also use imports, for example:
import java.util.*;

// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");

class Solution {
    public int[] solution(int[] A) {
        // write your code in Java SE 8
        int N = A.length;

        int[] answer = new int[N];
        // 0. 예외처리
        if( N < 2 ){
            answer[0] = 0;
            return answer;
        }

        // 1. A배열을 복사
        int[] copyA = Arrays.copyOfRange(A, 0, A.length);

        Arrays.sort(copyA);
        int[] table = new int[2*N + 1];

        int overNum = 0;
        int sameNum = 0;
        int prev = 2 * N + 1;
        for( int i=N-1; i>=0; i-- ){
            if( table[copyA[i]] != 0 ) {
                overNum += 1;
                continue;
            }

            if( prev == copyA[i] ){
                sameNum += 1;
            }else{
                sameNum = 0;
            }

            int nonNum = 0;
            // 아래에 있는 수만 파악
            for( int j=0; j<i; j++ ){
                if( copyA[i] == copyA[j] ) break;

                if( copyA[i] % copyA[j] != 0 ){
                    nonNum += 1;
                }
            }

            table[copyA[i]] = nonNum + overNum - sameNum;

            overNum += 1;
            prev = copyA[i];
        }

        for( int i=0; i<N; i++ ){
            answer[i] = table[A[i]];
        }

        return answer;
    }
}

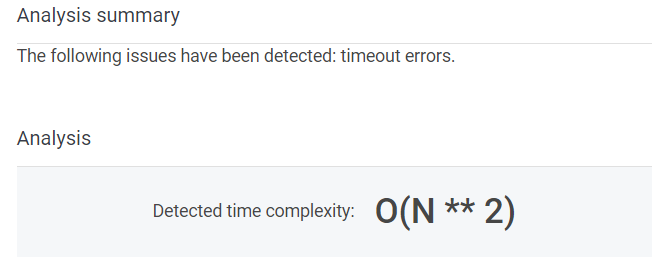
0.6xx였는데 조금 빨라짐..ㅠ

 

결국 구글링..

 

http://chienchikao.blogspot.com/2017/10/codility-lesson-11-sieve-of_21.html

Codility - Lesson 11 Sieve of Eratosthenes - 2. CountNonDivisible

 

https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=mares76&logNo=221299765860&categoryNo=54&proxyReferer= 

[Codility][Lesson11-2] CountNonDivisible

https://sustainable-dev.tistory.com/31

Codility Lesson11 - CountNonDivisible

 

3번째 블로그를 보니 이해함.. A배열 안에서 약수의 개수를 구하는게 핵심이였던 문제...( 그 이전에 약수의 개수를 구하는 것을 기억해야하는데... 바보다ㅠ )

 

구글링 후 3트...

- 약수의 개수를 구하고 전체 배열의 개수를 카운트 한 것과 연계하여 풀이

// you can also use imports, for example:
import java.util.*;

// you can write to stdout for debugging purposes, e.g.
// System.out.println("this is a debug message");

class Solution {
    public int[] solution(int[] A) {
        // write your code in Java SE 8

        int N = A.length;
        int[] answer = new int[N];
        if( N < 2 ){
            answer[0] = 0;
            return answer;
        }

        // 1. A배열의 수들이 몇개 있는지 카운트할 배열 생성
        int[] table = new int[2*N + 1]; // 제한조건에 의해서 2*N + 1가 됨

        // 2. A배열의 수 카운트
        for( int i=0; i<N; i++ ){
            table[A[i]] += 1;
        }

        // 3. 약수의 개수 세기
        for( int i=0; i<N; i++ ){ // 배열 개수만큼 반복
            int divider = 0;
            // System.out.println("i : " + i );
            for( int j=1; j*j<=A[i]; j++ ){
                if( A[i] % j == 0 ){
                    divider += table[j]; // 배열 A가 가지고 있는 원소 개수 만큼 더해줌
                    // System.out.println("divider : " + divider);
                    if( A[i] / j != j ){    // j와 같을 경우에는 같은 수가 됨으로 제외
                        System.out.println("divider : " + divider);
                        divider += table[ A[i]/j ];
                    }
                }
            }
            // System.out.println("divider : " + divider);
            answer[i] = N - divider;
        }

        return answer;
    }
}